How can we climb a tree structure?

These days I was writing a solution for a challenge in the HackerRank and I ended up writing a algorithm to walk through a tree structure. Nothing too special but I decided to white an article about the algorithms we can use.

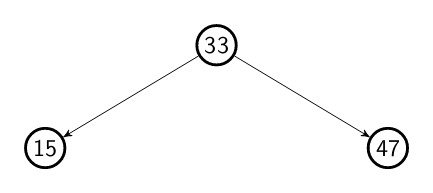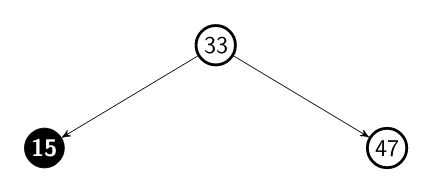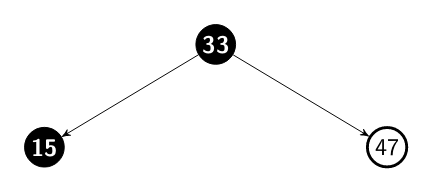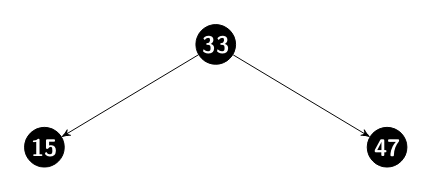
There are many types of tree out there. But to keep the simplicity, will not cover some aspects like balanced trees, add node, remove a node, delete a section of the tree, among other things. Let's focus how to walk through trees. In this article we will use the following tree structure in our examples:

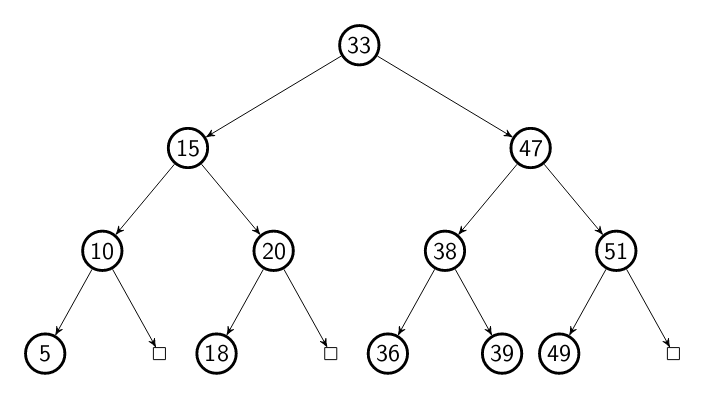
What's a tree?

Before see how to climb a tree, we need to define what is a tree in the first place. We can say that a tree is kind of a graph. But we will not cover graphs in depth here. So, let's not been so pedantic and use a more simple definition. We can say that a tree is compose of bunch of nodes connected with a parent/children relationship. What's a node? Well, a node is a data structure with a value, and a list of children nodes.

A node in a tree may have none, one, two or many children nodes. In this article we will focus on binary tree. Which means that the nodes in our tree will have 2 children nodes at most. As you can see in the tree shown before, no node has more than 2 children.

In our example, the value of each node is a integer. But it can be anything, even another tree. This will vary depending of application. In our tree the node 33 is the root node. The root node is the node which has no parent, it's the topmost node. All the algorithms show in the article start in the root node. The nodes 5, 18, 36, 39 and 49 are the leaf nodes. Leaf nodes has not children.

Algorithms

The following section describe the 3 main ways you can visit the nodes in a tree. You will see a gif showing the order in each node is visited. Black nodes mean that it has been visited. The main algorithms covered is preorder, inorder and posorder. Their names came from the relative root position with respect to its sub trees. Thus, preorder root node come first. posorder the root node is the last to be visited. inorderthe root node is visited between its left and right sub trees.

The 3 following algorithms visit each node once. Thus, their running time is O(n)

Preorder traversal

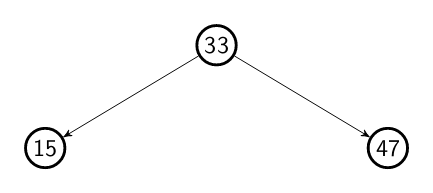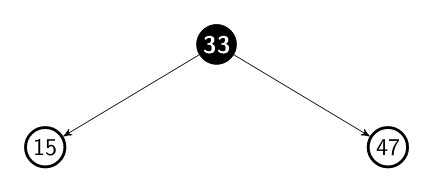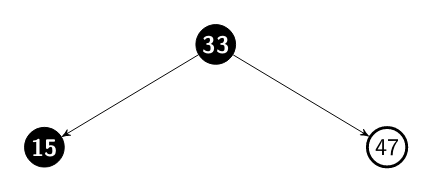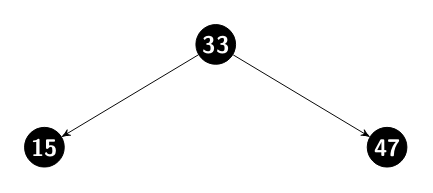
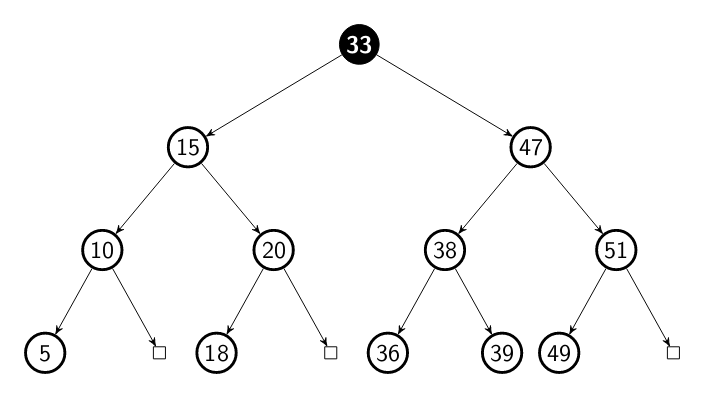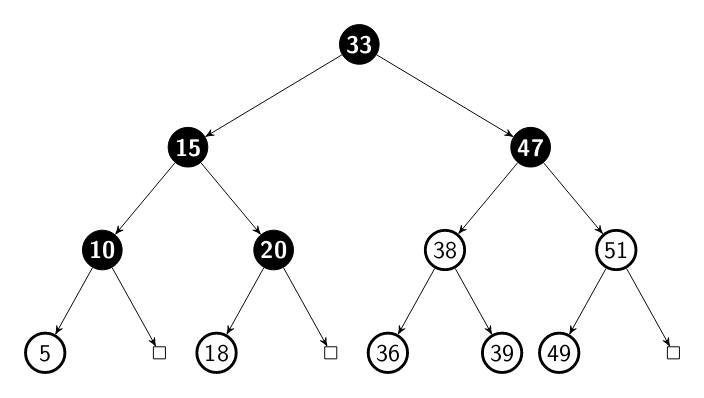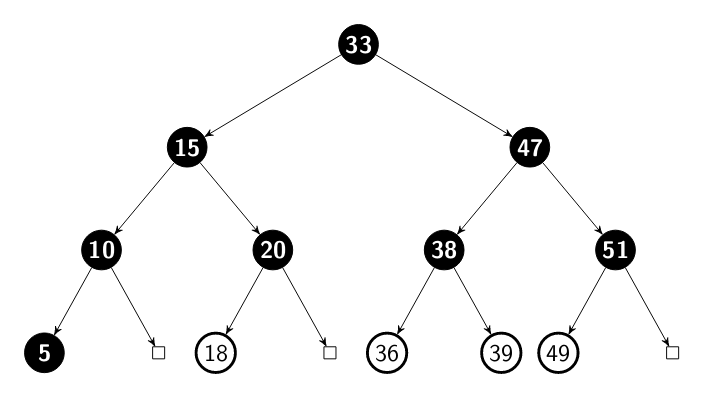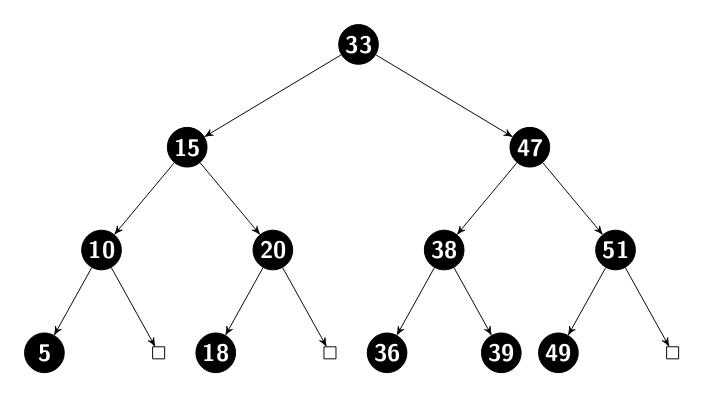
Ok, let's start with the pre order traversal. In this algorithm, as the name suggests, we visit the tree nodes in the following order: root, left, right. When we walk though a tree using the pre order traversal we fist visit the root node, the current node which we are sitting on. Then, we visit the node in the left and by consequence the whole sub tree. After that, we do the same with the right node and its sub tree. Considering our tree, the nodes would be visited in the following order: 33 15 10 5 20 18 47 38 36 39 51 49.

A possible recursive pseudocode this algorithms is:

// preorder the root come before its subtrees
def preorder-traversal(root):
    if root == null:
        return
    visit(root)
    preorder-traversal(root.left)
    preorder-traversal(root.right)

Posorder traversal

When we walk though a tree using the pos order traversal we fist visit the left, the right node and their sub tree and then the root node. If we run this algorithm using our tree as the input, the visit would be: 5 10 18 20 15 36 39 38 49 51 47 33

A possible recursive pseudocode this algorithms is:

// posorder the root come after its subtrees
def posorder-traversal(root):
    if root == null:
        return

    posorder-traversal(root.left)
    posorder-traversal(root.right)
    visit(root)

Inorder traversal

When we walk though a tree using the in order traversal we fist visit the left, the root and then right node and its sub tree. If we run this algorithm using our tree as the input, the visit would be: 5 10 15 18 20 33 36 38 39 47 49 51

A possible recursive pseudocode this algorithms is:

// inorder the root come between its subtrees
def inorder-traversal(root):
    if root == null:
        return

    inorder-traversal(root.left)
    visit(root)
    inorder-traversal(root.right)

Level order traversal

Different from the previous traversals this algorithm does not walk though the tree following the children nodes. It walk though the tree by level. This means that all the node in the same level as visit before move to the next level in the tree. Still using our tree as input example, this is the output: 33 15 47 10 20 38 51 5 18 36 39 49

I would say we can consider that level order traversal a variation of the preorder algorithm. The difference here is that we will use an auxiliary queue to visit the node. But it will continue visiting the nodes in the preorder. Take a look in the pseudocode here:

def level-order(root):
    queue q;
    q.push(root)
    while (q is not empty):
        visit(q.top)
        q.push(q.top.left)
        q.push(q.top.right)
        q.pop()

Just a quick note. Remember, a tree is a graph. Thus, we can consider the level order traversal as a breadth first search. The previous algorithms (preorder, posorder and inorder) are depth first search. Because they go as depth as possible first. ;-)

Vertical order traversal

The vertical order traversal, differently from the previous traversals and as the name suggests, walk through our tree in a vertical order. This means that, instead of visiting all the left, root or right node first, it visit all the nodes in the same horizontal distance from the root.

Horizontal distance

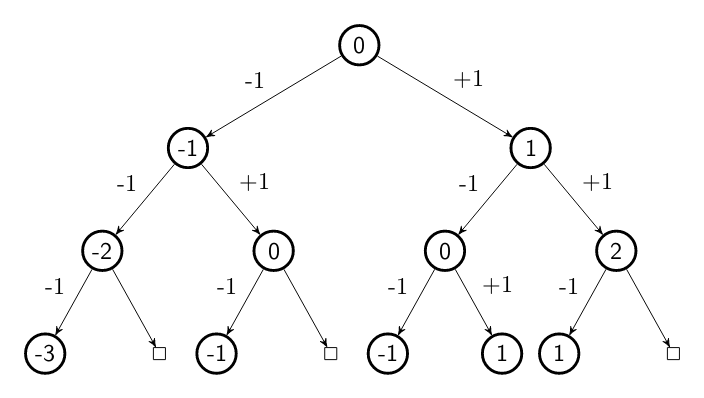
The horizontal distance (HD) of a node in the tree is the distance from the root node following this rules:

• The HD of the root node is 0;
• When move to a node in the left, subtract one (-1) from the distance;
• When move to a node in the right, add one (+1) from the distance;

Let's take a look in the HD for each node from the previous tree:

Coming back to our example tree and considering that we are using a preorder algorithm. This means that our tree will be visit in the following order:

5       // HD -3
10      // HD -2
15 18 36    // HD -1
33 20 38    // HD 0
47 39 49    // HD 1
51      // HD 2

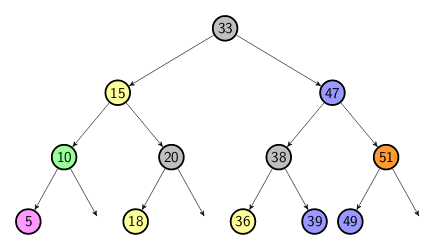
If we give different colors for each HD, we can visualize the tree as the fillowing:

Again, a pseudocode can be:

// function to find the horizontal distances of each nodes
def get-vertical-distances(distances, root, distance):
    if root is nil
        return
    // add the node in the node list for its HD
    distances[distance].append(root) 
    // recursive call in the left sub tree
    get-vertical-distances(distances, root.left, distances-1) 
    // recursive call in the right sub tree
    get-vertical-distances(distances, root.right, distances+1) 


// vertical order traveral
def vertical-order(root):
    // map to store the node with the same HD
    map<hd, list<nodes>> distances
    // find the nodes HD and populate the map
    get-vertical-distances(distances, root, 0)
    // visit the node by their distance
    for each distance in distances:
        for each node in distance:
            visit(node)

That's all for now!

As always if you saw something wrong or know how to improve the article. Please, let me know. Thanks!

References

I have some simple implementation of this algorithms in my sandbox repository. If you're interested in C++ and a real implementation of these algorithms, you are welcome to check it out. It's not something to be used in production, but you can take a look and show me if I'm doing something wrong! :)

I've used Latex to create the trees for this article: Example: Red-black tree

If you interested in more depth material. These books can be useful:

The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd Edition

Introduction to Algorithms, 3rd Edition

Algorithms Illuminated: Part 1: The Basics